INTRODUCTION
The ability to estimate total energy expenditure (TEE) accurately is frequently desired by athletes and practitioners alike. Access to this information can help in the design of optimal fuelling strategies for training and competition, supporting training adaptation and performance [1]. There are three components of TEE: resting energy expenditure (REE), thermic effect of exercise and diet induced thermogenesis. Basal metabolic rate (BMR) and REE are often used as interchange terms but, represent different concepts. BMR is defined as the minimal amount of energy to maintain the vital functions such as respiration, heartbeat, normal body temperature while, REE represents the energy to maintain the body functions at rest. Briefly, the assessment of BMR requires more standardized conditions and it is more challenging to measure than REE [2]. REE among athletes needs particular attention given the substantial contribution of REE to determine TEE [3]. Additionally, REE has been used as a parameter to define energy deficiency in sport participants [4]. Considering the preceding, the measurement of REE needs to follow a standardized protocol. The REE is typically obtained during the morning from continuous measures of VO2 and VCO2 at rest and athletes are instructed to avoid exercise 12 hours before REE testing. The participant is positioned in the supine position for 30–45 minutes with a mask or mouthpiece attached and then, 5–10 additional minutes of VO2 and VCO2 measures are obtained to assess REE [2]. The mentioned protocol requires considerable equipment, time, exercise restriction and knowledge [2]. Therefore, indirect estimations of REE have been for non-sport participants [5] and athletes [3].
The Harris-Benedict [6] and Cunningham [7] equations emerged as potential predictive estimations of REE in athletes [1]. Additionally, metabolic active tissue, expressed by fat-free mass (FFM) or lean soft tissue (LST), accounted for 60–70% of REE [8] and by inference should be considered a key factor in estimation of REE. The Harris-Benedict equation [6] did not measure metabolic active tissues while in the Cunningham equation [7] lean body mass was estimated based on body mass and age. The Harris-Benedict equation was developed 124 years ago, in 239 healthy participants (136 males, 103 female) and incorporated age, stature and body mass as explanatory predictors [6]. In parallel, Cunningham reanalysed the data of 223 participants from Harris and Benedict [6] and excluded 16 trained athletes. In this equation, estimated lean body mass accounted for 70% of REE [7]. Interestingly, both equations are systematically used to estimate REE but, they are not specifically design for athletes. Consequently, the generalization and application of these equations among athletes are questionable.
The development and application of athletic-specific and sport-specific equations has not received much consideration within sports nutrition literature although it has been previously recognized that population specific estimations are needed [1]. Multiple equations to predict REE has been developed among athletes that participated in different sports [9–11]. Nevertheless, the validation of sport-specific equations to estimate REE in independent samples is lacking. Considering the contribution of REE to estimate TEE and the frequent use of equations validated in general population in sport participants, the aim of this systematic review is to compare estimated REE with measured REE in athletes. This review also summarized the models used in athlete populations.
MATERIALS AND METHODS
The present systematic review followed the Cochrane guidelines [12] and it was conducted according to Preferred Reporting Items for Systematic Review (PRISMA) instructions [13].
Eligibility criteria
The manuscripts included in the current systematic review followed PICO (population, intervention, comparator and outcome) criteria [12]: population comprised of participants involved in organized sport; intervention was defined as REE measured by calorimetry – requirements for REE assessment needed to be described; equations to predict REE were used as a comparator; outcomes described comparisons between REE measured and REE estimated or potential equations to predict REE; cross-sectional and cohort studies were included in this review. Published manuscripts or abstracts in English were considered for the present study. No filter was applied to year of publication. Manuscripts that did not presented descriptive statistics for REE were eligible to the review because provide qualitative information about the accuracy of equations. Authors of the papers included in the review were contacted where relevant data were not present within the manuscript.
Information source and search strategy
Three electronic databases were consulted (i.e. Web of Science all databases, PubMed and Scopus) prior to 1th January of 2022. The search strategy included the keywords: (“resting energy expenditure” OR “resting metabolic rate” OR “basal metabolic rate” OR “basal energy expenditure” OR REE OR “basal metabolism”) AND (“predictive equation*” OR “prediction equation*” OR equation* OR prediction*) AND (athlete* OR sport*). Potential search terms were identified taking into account previous words used in the titles, abstract and keywords. Two specialists (DVM/AF) developed the search strategy that was supervised by an experienced author in systematic reviews and meta-analysis (HS). Afterwards, a reference manager software (EndNoteTMX9, Clarivate Analytics, Philadelphia, PA, USA) was used to export the studies.
Selection process
The initial screening by two independent authors (DVM and HS) according to the title and abstract. Then, full-text manuscripts were assessed to check if they met eligibility criteria. Discordances between authors were solved by consensus and if necessary a third independent reviewer (AF) was consulted.
Data collection process
Data extrapolation
Two authors (DVM/HS) extracted the information from eligible studies. Data was organized and summarized on adapted template of Cochrane Consumers and Communication Review Group [14]. The list of parameters included in the previous spreadsheet were: (1) number of participants, (2) sport, (3) sex, (4) age, (5) competitive level, (6) measurement of REE, (7) equation studied, (8) potential independent variables, (9) statistical parameters about the model, (10) main findings, (11) limitations. Among adolescent Brazilian soccer players [15], means and standard deviations of WHO/FAO/ UNU, Harris-Benedict, Henry and Cunningham equations were calculated consulting the supplementary material from the original study.
Data Items
The main outcomes extracted were categorized in two different groups: (1) measured and predicted REE; (2) equation to estimate REE. Moreover, any equation to predict REE was contrasted with measured REE. The agreement of predicted REE was determined within 5% or 10% intervals of the measured REE. Since authors anticipated that few equations to predict REE were developed among athletes, predictive models of REE were extracted and summarized as an outcome domain.
Study risk of bias
According to a recent study [16], the Quality Assessment Tool for Observational Cohort and Cross-Sectional Studies developed jointly the National Heart, Lung and Blood Institute (NHLBI) and Research Triangle Institute International to examine individually the quality of studies [17] and was implemented in the current manuscript. The tool included fourteen questions and an overall approach (i.e. good, fair or poor). Items reflecting the following parameters: (1) research question; (2,3) study population; (4) groups recruited from the same population and uniform eligibly criteria; (5) sample size justification; (6) exposure assessed prior to outcome of measurement; (7) sufficient timeframe to see an effect; (8) different levels of the exposure effect; (9) exposures measurement; (10) repeated exposure assessment; (11) outcomes measurement; (12) blinding of outcomes assessors; (13) follow-up rate; (14) statistical analysis. Two independent observers completed the tool (DVM/HS) and possible disagreements were solved by a third reviewer (AF).
RESULTS
Study selection
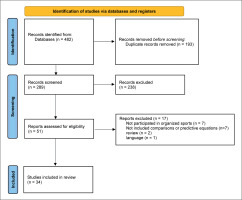
The databases searches identified 482 entries. Subsequently, duplicates were automatically and manually removed (n = 193). A total of 289 records were screened according to title and abstract, resulting in the exclusion of 238 records. The remaining 51 articles were read in full and 17 did not follow the eligible criteria: (1) the sample not clearly described as participants involved in organized sports (n = 7); (2) the manuscript did not show any comparison with equations or present a potential model for predicting REE (n = 7); (3) manuscripts were reviews (n = 2); (4) manuscript was not written in English (n = 1). Finally, 34 studies were selected to the current systematic review (Figure 1).
FIG. 1
Identification of studies via databases and registers.
From: Page MJ, McKenzie JE, Bossuyt PM, Boutron I, Hoffmann TC, Mulrow CD, et al. The PRISMA 2020 statement: an updated guideline for reporting systematic reviews. BMJ 2021;372:n71. doi: 10.1136/bmj.n71. For more information, visit: http://www.prisma-statement.org/
Study characteristics
The characteristics of studies (sample, age, stature, body mass, FFM or LST) included in the present review are summarized separately by age group and sex in Supplementary Table 1. Twenty-one and seven studies included male adult [4, 9–11, 18–34] and youth sport participants [15, 35–40], respectively. Female adult athletes participated in 19 studies [4, 10, 18, 19, 21–25, 30–34, 41–45] while, five studies used samples of young athletes [35, 37, 38, 40, 46].
Risk of bias in studies
Based on Quality Assessment Tool for Observational Cohort and Cross-Sectional Studies the risk of bias of studies was individually examined as shown in Supplementary Material 2. In general, studies did not estimate a priori sample size to examine differences between measured REE and estimated REE or to create an equation to extrapolate REE. In parallel, the inclusion criteria in each study were not described in some of the studies used in this systematic review. The overall quality rating of 28 studies was fair, 3 studies were classified as poor and 3 studies as good.
Results of individual studies
The comparison of measured REE with predicted values was noted in twelves studies of adults [4, 18, 19, 20, 21, 22, 26, 27, 30, 41, 42, 43] and analysed in seven studies of young athletes [15, 35, 36, 37, 38, 39, 46] as shown in Table 1. Of interest, Harris-Benedict, Cunningham and WHO/FAO/UNU were the main equations examined. Contrasting findings across studies are notable. For example, among ultra-endurance [21] and high-levels athletes [22], Harris-Benedict tended to underestimate measured REE while among Royal ballet dancers [4] predicted REE was overestimated in comparison to measured REE. Regarding the Cunningham equation, it tended to overestimate measured REE in Olympic male and female athletes [18] and underestimate measured REE in ultra-endurance athletes [21]. Predicted REE by WHO/FAO/UNU equation was, on average, substantially less than measured REE among Indian male weightlifters [26] and it was considered the most appropriate estimation of REE amongst adult male soccer players from Malaysia [24]. Overall, the equations developed to predict REE in general population were not comparable to measured REE in athletic samples. The percentage of agreement reported in six studies [10, 18, 21, 23, 33, 35] was often less than 60% for Harris-Benedict [10, 18, 21, 22, 23, 33] and Cunningham [21, 22] equations in athletes. Although sport-specific equations to estimate REE had received less attention, an agreement > 60% [10, 23, 25] was obtained in three studies that used De Lorenzo et al. [9] equation (Table 2). Studies which presented equations to estimate REE are summarized in Table 3 [9–11, 20, 22, 23, 25–28, 31, 34, 36, 37, 40, 43–45]. Body weight and FFM emerged as the most determinant predictors of REE. Two studies used the sum of four [44] and seven [28] body compartments to calculate REE in 93 collegiate athletes and 10 sumo wrestlers, respectively. Recently, two equations included somatotype [22] and phase angle [11] as potential determinants of REE.
TABLE 1
Mean ± standard deviation of measured REE and predicted REE considering alternative equations presented separately for adult and young athletes.
| Study | Sample | Sex | |||||
|---|---|---|---|---|---|---|---|
| Male | Female | ||||||
| REE measured (kcal · day−1) | Equation | REE predicted (kcal · day−1) | REE measured (kcal · day−1) | Equation | REE predicted (kcal · day−1) | ||
| ADULTS | |||||||
| Balci et al. [18] | Olympic athletes | 1885 ± 323 | Harris-Benedict | 1864 ± 180 | 1361 ± 232 | Harris-Benedict | 1483 ± 143 |
| Mifflin-BMSA | 1778 ± 138 | Mifflin-BMSA | 1425 ± 148 | ||||
| Mifflin-FFM | 1727 ± 149 | Mifflin-FFM | 1149 ± 111 | ||||
| Schofield | 1828 ± 186 | Schofield | 1466 ± 198 | ||||
| Cunningham (1991) | 1969 ± 167 | Cunningham (1991) | 1534 ± 124 | ||||
| Owen | 1644 ± 126 | Owen | 1325 ± 145 | ||||
| Liu | 1723 ± 180 | Liu | 1383 ± 184 | ||||
| De Lorenzo | 1911 ± 147 | De Lorenzo | 1597 ± 164 | ||||
| Bernstein | 1511 ± 154 | Bernstein | 1597 ± 128 | ||||
| Nelson | 1706 ± 201 | Nelson | 1339 ± 1635 | ||||
| Johnstone | 1838 ± 187 | Johnstone | 1229 ± 164 | ||||
| Roza | 1874 ± 85 | Roza | 1483 ± 69 | ||||
| Carlsohn et al. [19] | rowing and canoe racing | 2675 ± 526 | Harris-Benedict | 2133 ± 188 | 1577 ± 253 | Harris-Benedict | 1737±200 |
| Cunningham (1980) | 2260 ± 181 | Cunningham (1980) | 1734 ± 147 | ||||
| Cocate et al.[20] | cycling | 2051 ± 169 | Harris-Benedict | 1699 ± 95 | |||
| Schofield | 1699 ± 85 | ||||||
| FAO/WHO/UNU | 1702 ± 85 | ||||||
| Henry | 1562 ± 76 | ||||||
| Devrim-Lanpir | endurance sports | 2041 ± 301 | Harris-Benedict | 1701 ± 120 | 1788 ± 341 | Harris-Benedict | 1322 ± 82 |
| et al. [21] | Mifflin | 2038 ± 126 | Mifflin | 1602 ± 59 | |||
| Cunningham (1991) | 1894 ± 141 | Cunningham (1991) | 1497 ± 61 | ||||
| WHO/FAO/UNU – BMA | 1726 ± 86 | WHO/FAO/UNU – BMA | 1321 ±37 | ||||
| WHO/FAO/UNU – BM | 1755 ± 84 | WHO/FAO/UNU – BM | 1388 ± 41 | ||||
| Wang | 1744 ± 157 | Wang | 1289 ± 68 | ||||
| Sabounchi1 | 1743 ± 137 | Sabounchi1 | 1363 ± 62 | ||||
| Sabounchi1 | 1662 ±117 | Sabounchi1 | 1383 ± 56 | ||||
| Sabounchi1 | 1739 ± 89 | Sabounchi1 | 1158 ± 30 | ||||
| Freire et al. [22] | high level athletes | 2099 ± 400 | Harris-Benedict | 1896 ± 291 | 1577 ± 170 | Harris-Benedict | 1490±104 |
| ten Haaf – BM | 2082 ± 258 | ten Haaf – BM | 1573 ± 155 | ||||
| ten Haaf – FFM | 2243 ± 326 | ten Haaf – FFM | 1695 ± 139 | ||||
| WHO/FAO/UNU | 1975 ± 302 | WHO/FAO/UNU | 1429 ± 132 | ||||
| De Lorenzo | 2046 ± 242 | De Lorenzo | 1683 ± 165 | ||||
| Wong | 1969 ± 262 | Wong | 1505 ± 127 | ||||
| Jagim | 2435 ± 392 | Jagim | 1645 ± 205 | ||||
| Cunningham (1980) | 2170 ± 309 | Cunningham (1980) | 1650 ± 132 | ||||
| Cunningham (1991) | 2039 ±309 | Cunningham (1991) | 1519 ± 132 | ||||
| Joseph et al. [26] | weightlifting | 2217 ± 515 | Katch-McArdle | 1687 ± 198 | |||
| Cunningham (1980) | 1842 ± 202 | ||||||
| WHO/FAO/UNU | 1821 ± 226 | ||||||
| ICMR | 1727 ± 215 | ||||||
| Harris-Benedict | 1791 ± 221 | ||||||
| Mifflin | 1699 ± 172 | ||||||
| Owen | 1580 ± 148 | ||||||
| Nelson | 1294 ± 263 | ||||||
| Mackay et al. [41] | recreational and sub-elite athletes | 1452 ± 267 | Harris-Benedict | 1438 ± 113 | |||
| Mifflin | 1392 ± 140 | ||||||
| WHO/FAO/UNU | 1460 ± 133 | ||||||
| Mackenzie-Shalders et al. [27] | rugby | 2389 ± 263 | Cunningham | 2287 ± 176 | |||
| Harris-Benedict2 | 2242 ± 233 | ||||||
| Harris-Benedict2 | 2213 ± 226 | ||||||
| Marques et al. [42] | karate | 1689 ± 286 | WHO/FAO/UNU | 1401 ± 89 | |||
| Harris-Benedict | 1449 ± 54 | ||||||
| Cunningham (1980) | 1552 ± 122 | ||||||
| Henry | 1326 ± 69 | ||||||
| O'Neil et al. [43] | rugby | 1651 ± 167 | Cunningham (1980) | 1665 ± 124 | |||
| Harris-Benedict | 1545 ± 117 | ||||||
| ten Haaf – FFM | 1690 ± 129 | ||||||
| ten Haaf – BM | 1679 ± 166 | ||||||
| Jagim | 1830 ± 219 | ||||||
| Watson – FFM | 1520 ± 65 | ||||||
| Watson – BM | 1623 ± 99 | ||||||
| Sena et al. [30] | CrossFit | 1885 ± 416 | Harris-Benedict | 1869 ± 188 | 1403 ± 258 | Harris-Benedict | 1397 ± 108 |
| WHO/FAO/UNU | 1878 ± 154 | WHO/FAO/UNU | 1380 ± 105 | ||||
| Henry | 1708 ± 151 | Henry | 1307 ± 108 | ||||
| Cunningham (1980) | 2031 ± 165 | Cunningham (1980) | 1521 ± 126 | ||||
| Cunningham (1991) | 1873 ± 162 | Cunningham (1991) | 1373 ± 124 | ||||
| Mifflin | 1771 ± 147 | Mifflin | 1309 ± 164 | ||||
| Staal et al. [4] | ballet dancers | 1692 ±103 | Cunningham (1980) | 1967 ± 104 | 1215 ±106 | Cunningham (1980) | 1504 ± 108 |
| Harris-Benedict | 1896 ± 135 | Harris-Benedict | 1355 ± 127 | ||||
| Koehler | 1813 ± 73 | Koehler | 1378 ± 69 | ||||
| Tinsley et al. [31] | muscular physique | 2337 ± 3103 | Hayes | 2166 ± 199 | 1566 ± 1333 | Hayes | 1438 ± 126 |
| 2408 ± 3503 | Cunningham (1980) | 2245 ± 170 | 1633 ± 1823 | Cunningham (1980) | 1581 ± 107 | ||
| Cunningham (1991) | 2083 ± 167 | Cunningham (1991) | 1432 ± 105 | ||||
| Mifflin – FFM | 1975 ± 152 | Mifflin – FFM | 1381 ± 96 | ||||
| Mifflin – BM | 1944 ± 144 | Mifflin – BM | 1396 ± 95 | ||||
| Owen | 2058 ± 172 | Owen | 1302 ± 96 | ||||
| ten Haaf – FFM | 2290 ± 176 | ten Haaf – FFM | 1604 ± 110 | ||||
| ten Haaf – BM | 2192 ± 168 | ten Haaf – BM | 1566 ± 112 | ||||
| Harris-Benedict | 2086 ± 176 | Harris-Benedict | 1454 ± 70 | ||||
| WHO/FAO/UNU | 2102 ± 160 | WHO/FAO/UNU | 1417 ± 77 | ||||
| De Lorenzo | 2032 ± 180 | De Lorenzo | 1677 ± 107 | ||||
| Watson et al. [45] | National Collegiate Athletic Association (NCAA) collegiate athletes | 1466 ± 150 | Harris-Benedict | 1528 ± 98 | |||
| Schofield | 1483 ± 132 | ||||||
| Mifflin | 1472 ± 134 | ||||||
| Owen | 1278 ± 64 | ||||||
| WHO/FAO/UNU | 1496 ± 141 | ||||||
| Cunningham (1980) | 1588 ± 129 | ||||||
| Taguchi | 1366 ± 157 | ||||||
| Wong et al. [24] | elite athletes | 1715 ± 204 | WHO/FAO/UNU | 1690 ± 130 | 1384 ± 147 | WHO/FAO/UNU | 1311 ± 83 |
| Ismail | 1461 ± 130 | Ismail | 1185 ± 72 | ||||
| De Lorenzo | 1734 ± 111 | Cunningham (1980) | 1451 ± 81 | ||||
| Cunningham (1980) | 1760 ± 163 | Harris-Benedict | 1387 ± 57 | ||||
| Harris-Benedict | 1684 ± 140 | ||||||
| YOUTH | |||||||
| Cherian et al. [35] | IOM | 1308 ± 63 | |||||
| soccer | 1343 ± 297 | Cunningham (1980) | 1375 ± 197 | 1135 ±117 | Cunningham (1980) | 1252 ± 83 | |
| Henry | 1428 ± 205 | Henry | 1262 ± 73 | ||||
| Soares – BMA | 1357 ± 124 | Soares-FFM | 1135 ± 80 | ||||
| Soares – FFM | 1252 ± 190 | Patil-BM | 1085 ± 74 | ||||
| Patil – BM | 1402 ± 137 | Patil-BMSA | 1100 ± 77 | ||||
| Patil – BMSA | 1184 ± 186 | Wong | 1317 ± 119 | ||||
| De Lorenzo | 1429 ± 223 | ten Haaf: | 1263 ± 8 | ||||
| Wong ten | 1334 ± 201 | ||||||
| ten Haaf | 1390 ± 204 | ||||||
| Hannon et al. [36] | soccer | 1858 ± 215 | Cunningham (1980) | 1578 ± 281 | |||
| De Lorenzo | 1769 ± 263 | ||||||
| Henry | 1758 ± 272 | ||||||
| Kim | 1466 ± 191 | ||||||
| Wong | 1693 ± 193 | ||||||
| Loureiro et al. [38] | pentathlon | 1559 ± 203 | WHO/FAO/UNU | 1679 ± 152 | 1357 ± 140 | WHO/FAO/UNU | 1376 ± 110 |
| Harris-Benedict | 1610 ± 149 | Harris-Benedict | 1366 ± 89 | ||||
| Henry | 1667 ± 172 | Henry | 1279 ± 92 | ||||
| Cunningham (1980) | 1580 ± 171 | Cunningham (1980) | 1344±194 | ||||
| Łouszczki et al. [39] | soccer | 1844 ± 328 | Harris-Benedict | 1513 ± 256 | |||
| WHO/FAO/UNU | 1567 ± 260 | ||||||
| IMNA | 1662 ± 303 | ||||||
| Cunningham (1991) | 1450 ± 264 | ||||||
| Mifflin | 1481 ± 224 | ||||||
| Owen | 1413 ± 147 | ||||||
| Altman and Dittmer | 1534 ± 283 | ||||||
| Maffeis | 1368 ± 150 | ||||||
| Schofield | 1589 ± 253 | ||||||
| Molnar | 1469 ± 239 | ||||||
| De Lorenzo | 1520 ± 298 | ||||||
| Kim et al. [37] | soccer | 1648 ± 111 | Harris-Benedict | 1556 ± 58 | 1365 ± 186 | Harris-Benedict | 1418 ± 56 |
| WHO/FAO/UNU | 1577 ± 65 | WHO/FAO/UNU | 1431 ± 63 | ||||
| IMNA | 1538 ± 70 | IMNA | 1367 ± 65 | ||||
| Cunningham (1991) | 1677 ± 95 | Cunningham (1991) | 1309 ± 58 | ||||
| Mifflin | 1543 ± 78 | Mifflin | 1342 ± 76 | ||||
| Owen | 1284 ± 38 | Owen | 1198 ± 37 | ||||
| Altman and Dittmer | 1867 ± 101 | Altman and Dittmer | 1640 ± 98 | ||||
| Maffeis | 1470 ± 60 | Maffeis | 1321 ± 58 | ||||
| Schofield | 1593 ± 63 | Schofield | 1431 ± 62 | ||||
| De Lorenzo | 1826 ± 99 | De Lorenzo | 1564 ± 97 | ||||
| Park | 1648 ± 51 | Park | 1590 ± 365 | ||||
| Oliveira et al. [15] | soccer | 1717 ± 203 | WHO/FAO/UNU | 1854 ± 131 | |||
| Harris-Benedict | 1760 ± 126 | ||||||
| Henry | 1864 ± 148 | ||||||
| Cunningham (1980) | 1728 ± 129 | ||||||
FAO/WHO/UNU (Food and Agriculture Organization/World Health/United Nations University); IMNA (Institute of Medicine of the National Academies); ICMR (Indian Council of Medical Research); IOM (Institute of Medicine); BMA (body mass, age); FFM (fat-free mass); BM (body mass); BMSA (body mass, stature, age).
TABLE 2
Percentage of agreement and disagreement between measured REE and predicted REE.
| Study | n | equation | agreement | over-predicted | under-predicted |
|---|---|---|---|---|---|
| ADULTS – MALE | |||||
| Balci et al. [18] | 25 | Harris-Benedict | 40% | 36% | 24% |
| Mifflin-BMSA | 40% | 24% | 36% | ||
| Mifflin-FFM | 60% | 8% | 32% | ||
| Schofield | 11% | 28% | 28% | ||
| Cunningham | 10% | 52% | 8% | ||
| Owen | 12% | 4% | 48% | ||
| Liu | 12% | 12% | 40% | ||
| De Lorenzo | 10% | 40% | 20% | ||
| Bernstein | 5% | 0% | 80% | ||
| Nelson | 15% | 8% | 32% | ||
| Johnstone | 13% | 24% | 24% | ||
| Roza | 6% | 44% | 32% | ||
| Devrim-Lanpir et al. [21]* | 15 | Harris-Benedict | 20% | 7% | 73% |
| Mifflin | 47% | 27% | 27% | ||
| Cunningham | 47% | 33% | 20% | ||
| WHO/FAO/UNU – BMA | 20% | 7% | 73% | ||
| WHO/FAO/UNU – BM | 20% | 7% | 73% | ||
| Wang | 27% | 7% | 67% | ||
| Sabounchi1 | 27% | 7% | 67% | ||
| Sabounchi1 | 13% | 7% | 80% | ||
| Sabounchi1 | 20% | 7% | 73% | ||
| Freire et al. [22]** | 58 | Harris-Benedict | 36% | ||
| ten Haaf – BM | 45% | ||||
| ten Haaf – FFM | 29% | ||||
| FAO/WHO/UNU | 33% | ||||
| De Lorenzo | 38% | ||||
| Wong | 29% | ||||
| Jagim | 7% | ||||
| Cunningham (1980) | 50% | ||||
| Cunningham (1991) | 50% | ||||
| Freire et al. [22]* | 58 | Harris-Benedict | 67% | ||
| ten Haaf – BM | 72% | ||||
| ten Haaf – FFM | 59% | ||||
| FAO/WHO/UNU | 64% | ||||
| De Lorenzo | 69% | ||||
| Wong | 64% | ||||
| Jagim | 24% | ||||
| Cunningham (1980) | 71% | ||||
| Cunningham (1991) | 78% | ||||
| Frings-Meuthen et al. [23] | 79 | Harris-Benedict | 48% | 0% | 52% |
| FAO/WHO/UNU | 63% | 0% | 37% | ||
| Muller | 66% | 6% | 28% | ||
| Muller-FFM | 66% | 1% | 33% | ||
| Cunningham | 68% | 25% | 7% | ||
| De Lorenzo | 72% | 10% | 18% | ||
| ten Haaf and Weijs [10]* | 53 | Cunningham | 84.9% | ||
| De Lorenzo | 77.4% | ||||
| Van Grouwn etal. [33]* | 16 | Mifflin | 56.3% | ||
| Harris-Benedict | 43.8% | ||||
| ADULTS – FEMALE | |||||
| Balci et al. [18] | 24 | Harris-Benedict | 50% | 42% | 8% |
| Mifflin | 71% | 17% | 13% | ||
| Mifflin | 58% | 17% | 25% | ||
| Schofield | 54% | 38% | 8% | ||
| Cunningham | 54% | 38% | 8% | ||
| Owen | 38% | 58% | 4% | ||
| Liu | 67% | 21% | 12% | ||
| De Lorenzo | 42% | 58% | 0% | ||
| Bernstein | 17% | 8% | 75% | ||
| Nelson | 33% | 8% | 58% | ||
| Johnstone | 54% | 29% | 17% | ||
| Roza | 38% | 63% | 0% | ||
| Devrim-Lanpir et al. [21]* | 15 | Harris-Benedict | 13% | 0% | 87% |
| Mifflin | 53% | 13% | 33% | ||
| Cunningham | 20% | 13% | 67% | ||
| WHO/FAO/UNU – BMA | 13% | 0% | 87% | ||
| WHO/FAO/UNU – BM | 27% | 0% | 73% | ||
| Wang | 13% | 0% | 87% | ||
| Sabounchi (2013)1 | 20% | 0% | 80% | ||
| Sabounchi (2013)1 | 27% | 0% | 73% | ||
| Sabounchi (2013)1 | 7% | 0% | 93% | ||
| Freire et al. [22]** | 44 | Harris-Benedict | 30% | ||
| ten Haaf – BM | 39% | ||||
| ten Haaf – FFM | 25% | ||||
| FAO/WHO/UNU | 25% | ||||
| De Lorenzo | 36% | ||||
| Wong | 36% | ||||
| Jagim | 39% | ||||
| Cunningham (1980) | 41% | ||||
| Cunningham (1991) | 43% | ||||
| Freire et al. [21]* | 44 | Harris-Benedict | 59% | ||
| ten Haaf – BM | 66% | ||||
| ten Haaf – FFM | 59% | ||||
| FAO/WHO/UNU | 57% | ||||
| De Lorenzo | 75% | ||||
| Wong | 68% | ||||
| Jagim | 59% | ||||
| Cunningham (1980) | 70% | ||||
| Cunningham (1991) | 73% | ||||
| Frings-Meuthen et al. [23] | 34 | Harris-Benedict | 47% | 3% | 50% |
| FAO/WHO/UNU | 41% | 6% | 53% | ||
| [23] | Muller | 47% | 3% | 50% | |
| Muller-FFM | 46% | 3% | 52% | ||
| Cunningham | 64% | 36% | 0% | ||
| De Lorenzo | 62% | 27% | 12% | ||
| ten Haaf and Weijs [10] | 37 | Cunningham | 78.4% | ||
| De Lorenzo | 59.5% | ||||
| Van Grouwn et al. [33]* | 17 | Mifflin | 82.2% | ||
| Harris-Benedict | 52.3% | ||||
| YOUTH | |||||
| Cherian et al. [35]* | male | 21 | Cunningham | 71.4% | |
| Henry | 57.1% | ||||
| Soares – BMA | 61.9% | ||||
| Soares – FFM | 42.9% | ||||
| Patil – BMA | 61.9% | ||||
| Patil – BMSA | 38.1% | ||||
| De Lorenzo | 61.9% | ||||
| Wong | 76.2% | ||||
| ten Haaf | 66.7% | ||||
| Cherian | female | 19 | Cunningham | 42.1% | |
| Henry | 47.9% | ||||
| Soares | 94.7% | ||||
| Patil – BMA | 78.9% | ||||
| Patil – BMSA | 89.5% | ||||
| Wong | 21.1% | ||||
| ten Haaf | 42.1% | ||||
TABLE 3
Equations developed among athletes to estimate REE.
| Study | sex | sample | Equation REE |
|---|---|---|---|
| Cocate et al. [20] | male | cycling | REE = -12888.2 + 485.846 × FFM – 3.7846 × FFM2–24.0092 × age |
| De Lorenzo et al. [9] | male | water polo, judo, karate | REE = -857 + 9.0 × body mass + (11.7 × stature |
| Freire et al. [22] | male and female | high level athletes | REE = 729.50 + 175.64 × sex – 7.23 × age + 15.87 × body mass + 1.08 × stature REE = -2688.12 + 521.08 × sex + 42.86 × age + 18.98 × body mass + 16.76 × stature + 85.47 × mesomorphy + 140.54 × endomorphy – 8.24 × body mass × sex + 1.53 × body mass × endomorphy – 0.65 × body mass × age |
| Frings-Meuthen et al. [23] | male and female | master athletic athletes | REE = -222.088 + 18.577 × FFM + 6.753 × FM + 23.910 × temperature + 78.479 × sex |
| Hannon et al. [36] | male | youth soccer | REE = 1315 + 11.1 × FFM REE = 1254 + 9.5 × body mass |
| Jagim et al. [25] | male and female | National Collegiate Athletic Association (NCAA) collegiate athletes | REE = 19.46 × body mass + 775.33 (males) REE = 21.10 × body mass + 288.6 (females) |
| Joseph et al. [26] | male | weightlifting | REE = -164.065 + 0.039 × LBM |
| Kim et al. [37] | male and female | youth soccer | REE = 502.7 + (8.6 × body mass) + (9.7 × VO2max) REE = 730.4 + 15 × FFM |
| Marra et al. [11] | male | elite athletes | REE = 17.2 × body mass – 5.95 × age + 748 REE = 16.3 × body mass + 95.4 × phase angle – 93 |
| MacKenzie-Shalders et al. [27] | male | rugby | REE = 29.71 × LBM – 24.56 (beginning of pre-season) REE = 26.75 × LBM + 145.44 (prior to competition) |
| Midorikawa et al. [28] | male | sumo wrestlers | REE* = (13 × skeletal muscle mass) + (4.5 × adipose tissue mass) + (240 × brain mass) + (200 × liver mass) + (440 × kidney mass) + (440 × heart mass) + (12 × residual mass) |
| O’Neil et al. [43] | female | rugby | REE = 649.6 + 18.91 × FFM REE = 150.1–6.858 × age – 2.946 × stature + 11.21 × body mass |
| Reale et al. [40] | male and female | different sports | REE = body mass × 11.1 + stature × 8.4–339.7 (males) REE = FFM × 14.5 + FM + 8.6 + stature × 5.7–35.9 (males) REE = body mass × 11.1 + stature × 8.4–537.1 (females) REE = FFM × 14.5 + FM + 8.6 + stature × 5.7–203.9 (females) |
| Taguchi et al. [44] | female | collegiate athletes | REE = 17.8 × body mass + 243 REE = 26.9 × FFM + 36 REE* = (2.3 × body mass) + (4.5 × adipose tissue) + (13 × skeletal muscle) + (54 × residual mass) |
| ten Haaf and Weijs [10] | male and female | different sports | REE = 11.936 × body mass + 587.7 x stature – 8.129 × age + 191.027 × sex + 29.279 REE = 22.771 × FFM + 484.264 |
| Tinsley et al. [31] | male and female | muscular physique | REE = 25.9 × FFM + 284 REE = 24.8 × body mass + 10 |
| Watson et al. [45] | female | National Collegiate Athletic Association (NCAA) collegiate athletes | REE = 88.1 + 2.53 × stature + 8.42 × body mass + 19.46 × age REE = 120.81 + 4.88 × stature + 8.24 × FFM + 5.71 × age |
| Wong et al. [34] | male and female | elite athletes | REE = 669 + 13 × body mass + 192 × sex |
DISCUSSION
The aim of the present study was to review the agreement between measured REE and predicted REE using estimative equations. Additionally, the current systemic review summarized estimations of REE obtained using participants involved in organized sports. In general, across different samples of sport participants, measured REE was not comparable with REE predicted from equations developed in general population. Consistent results were noted among participants classified as overweight and obese [47] as well in healthy older adults aged ≥ 60 years [24]. Two equations, De Lorenzo et al. [9] and ten Haaf and Weijs [10], included athletes from different sports. Although few studies tested the precision of these equations, an agreement of 72% and 68% was noted with measured REE in male [23] and female [22] athletes, respectively. Therefore, the De Lorenzo and ten Haaf equations seems to be acceptable alternatives to estimate REE in athletes. Although Harris-Benedict and Cunningham equations were claimed to estimate REE among athletes, population-specific equations are needed [1].
Among 49 Turkish Olympic athletes differences between measured REE and predicted REE by Harris-Benedict equation were, on average, negligible however, only 40% and 50% of males and females, respectively, were within 10% of the measured REE [18]. Conversely studies using the Cunningham equation provided inconsistent results – underestimating REE in 83% of adolescent athletes aged 13–19 years [40] while, among 90 adult sport participants [10] an acceptable agreement between measured REE and predicted REE was reported in males (84.9%) and females (78.4%). Recently, the application of the Cunningham equation was recommended for use in female athletes but not be considered in males [24]. The equation explained 34% of variance in measured REE and an error 15% of with Cunningham model was noted among males [24]. In general, predicted REE by the Cunningham equation should not be generalized for athletic samples. This equation estimated lean body mass based on age and body mass [48]. Studies about REE estimation in athletes applied different methods to determine body composition. ten Haaf and Weijs [10] used air displacement plethysmography technique in 90 adult athletes while a recent study in Premier League soccer academy athletes used DXA methodology obtain FFM [36]. Considering the preceding, few studies that analysed Cunningham equation adopted the same methodology to estimate metabolic active tissues as original author [7]. The Cunningham equation was reviewed in 1991 but inconsistent results to predict REE were also noted [49].
The Mifflin equation [50] also emerged as a potential model to provide sex-specific estimates of REE in sport [51]. Fat mass and FFM were estimated from skinfold subcutaneous adipose tissue measurements [52, 53] and final sex-specific equations incorporated age, body mass and stature. The original sample included 247 females (ranging 20–76 years-old) and 251 males (age ranging 19–78 years-old). Of those, 112 females and 122 males were classified as obese [50]. Not surprisingly, predicted REE by the Mifflin equation tended to underestimate -114 kcal and -94 kcal measured REE among males and females CrossFit athletes, respectively [30]. In a sample of 9 power-lifters and 3 weightlifters Mifflin equation differed 11% of measured REE and it was supported that WHO/ ONU/UNU should be used to predict REE [29]. The sample of WHO/ ONU/UNU derived from the 7173 European and North American data points. Even though 3338 data points were obtained from active Italian participants with an elevated REE [54] this equation seems to be not applicable in athletes. Differences between measured REE and predicted REE using WHO/ONU/UNU equation ranged 466–287 kcal · day−1 in 30 ultra-endurance athletes aged 23–55 years [21]. Overall, the equations developed in general population should not be generalized for participants involved in organized sport. As a result, studies involving athletes proposed new predictive models to estimate REE.
Two potential equations to predict REE among athletes [9, 10] were compared with indirect calorimetry. Based on 126 male elite athletes from different sports minimal differences (21 kcal · day−1 and 60 kcal · day−1) were reported between the De Lorenzo et al. [9] and ten Haaf and Weijs [10] equations and measured REE [11]. The latter equation successfully predicted REE (within ± 10%) in 31 out of 36 female adult rugby players [43]. However, REE was underestimated by the De Lorenzo equation in young male soccer players [34, 36]. Three particular issues need highlighting: (1) De Lorenzo and ten Haaf models were validated in sport participants but received little consideration in sports nutrition literature and practice; (2) both equations combined adult athletes from different sports; (3) equations were developed in adults should not be generalized for youth sport participants.
Although the considerable number of studies extracted in the current review, a possible limitation is the inclusion of only English records. Additionally, grey literature was not also considered. Only one estimated a priori sample size necessary to create predictive models of REE. Future studies need to cross-validate the equations which used athletes from different modalities in larger sport-specific samples. Of note, predictions of REE only using female athletes are available in the literature and future research is required. The sex-specific equation proposed by ten Haaf and Weijs [10] is also adequate to predict REE in female athletes. The equation developed by De Lorenzo et al. [9] only included male participants from different sports hence, it is a valid alternative to estimate REE in male athletes. Specific equations were developed for youth involved in different sports [16] and soccer players [39, 44] thereby, should be adopted in studies of young athletes.
Findings of current review are crucial for nutritionists and/or staff providing nutrition support within sport in order to optimise total daily energy intake. The use of indirect equations in athletes, especially those that were developed in general population, tended to produce different values of measured REE which in turn has impact on TEE (obtained by multiplying REE and an appropriate physical activity factor). In summary, De Lorenzo et al. [9] and ten Haaf and Weijs [10] seem to be the most appropriate equations to predict REE among adult athletes and needed particular attention by sport nutritionists. Validation of predictive models to estimate REE required future research particularly in sport-specific samples and youth athletes.








